1. Fontes de dados

Antes de tudo, vamos coletar todos os arquivos que irão nos fornecer os dados necessários para esse modelo. São eles: 

Arquivo CadUsH

• Pode ser encontrado em: Sintegre > Programação da Operação > [Médio Prazo] Notas Técnicas – Médio Prazo > CadUsH.csv; 
• Fornece os dados de cadastros da UHEs. 

Planilha Vazões_Mensais_1931_2023 

• Pode ser encontrada em: Sintegre > Programação da Operação > [Séries Históricas de Vazões Naturais] Séries Históricas de Vazões Naturais > Vazões_Mensais_1931_2023.xls; 
• Fornece a MLT das UHEs. 

Planilha Pilha_term_PMO 

• Pode ser encontrada em: Sintegre > Programação da Operação > [Médio Prazo] Notas Técnicas – Médio Prazo > Pilha_term_PMO; 
• Fornece o empilhamento térmicos das UTEs. 

RDH 

• Pode ser encontrada em: Sintegre > Programação da Operação > RDH; 
• Fornece o volume inicial das UHEs (%). 

2. Iniciando o modelo

O primeiro passo agora é obter os dados referentes à nossa UHE no arquivo CadUsH.csv. Para ilustrar o processo, vamos selecionar a UHE Furnas. Na imagem 1 podemos ver destacadas quais colunas foram utilizadas para obter os dados necessários.

O segundo passo é criar uma planilha Excel para receber o nosso modelo. Vamos organizar os dados necessários da nossa UHE nessa planilha, nas colunas A, B e C conforme é mostrado na Imagem 2.

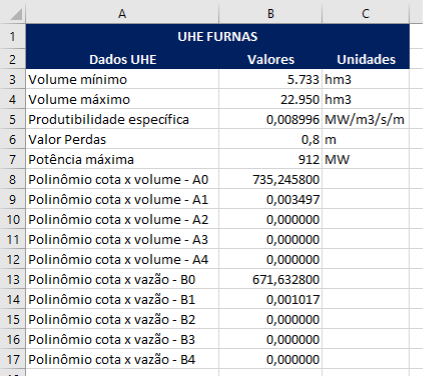
Feito isso vamos agora iniciar a construção da tabela de cálculos do nosso modelo. No exemplo eu utilizei a mesma planilha e iniciei a tabela de cálculos na coluna F.  

O primeiro elemento da tabela é o conjunto de períodos que desejamos planejar. Supondo que a análise será mensal e que queremos planejar a operação no horizonte de 1 ano a frente, montamos então as colunas conforme mostrado na Imagem 3.

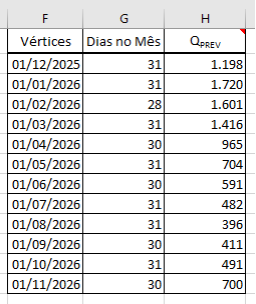
Vértices = preenchemos com cada mês do ano do nosso horizonte de planejamento. Estamos utilizando o dia 01 de cada mês apenas como referência temporal. 

Dias no Mês = aqui criamos uma fórmula no Excel para calcular automaticamente a quantidade de dias de cada mês. Essa informação será importante em etapas posteriores do nosso modelo. 

Vazão prevista (Qprev) = aqui inserimos os valores de vazão afluente previstos para a UHE em cada mês. Surge então a primeira dificuldade: como definir a vazão futura de cada período? Como a previsão hidrológica não é o foco da nossa modelagem, adotaremos uma abordagem simplificada: utilizaremos a Vazão Média de Longo Termo (MLT) de cada mês. Esses valores podem ser obtidos na planilha Vazões_Mensais_1931_2023, buscando pelo nome da usina selecionada, que no nosso caso é a UHE Furnas. 

3. Calculando a operação da UHE

Dando continuidade à construção do nosso modelo, vamos agora estruturar os cálculos de operação da UHE. Ao final desta etapa, devemos obter uma tabela semelhante à apresentada na Imagem 4, contendo as seguintes colunas:

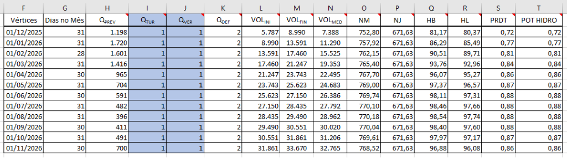
Vazão Turbinada (Qtur) = corresponde a vazão utilizada para a geração de energia. Esse valor será definido posteriormente pelo algoritmo de otimização do Excel. Por ora, vamos preencher com um valor qualquer provisório, como o número 1, e deixar esse campo com outra cor para destacar. 

Vazão Vertida (Qver) = corresponde a vazão que será vertida, ou seja, que será escoada através da UHE sem gerar energia. Esse valor também será definido posteriormente pelo algoritmo de otimização do Excel. Por ora, vamos preencher com um valor qualquer provisório, como o número 1, e deixar esse campo com outra cor para destacar. 

Vazão defluente (Qdef) = corresponde a vazão total que sai da UHE, sua fórmula é bastante simples:  Qdef = Qtur + Qver . 

Volume inicial (VOLini) = corresponde ao volume do reservatório no início de cada mês. O valor do primeiro estágio, no nosso caso o valor de dez/2025, deve ser informado ao modelo. Veremos mais adiante como podemos obter esse valor. Já os valores dos demais estágios são iguais aos valores do volume final do estágio anterior. Exemplo: o volume inicial de jan/2026 é igual ao volume final de dez/2025. 

Volume final (VOLfin) = corresponde ao volume do reservatório no final do mês, calculado por: 

VOLfin = VOLini+(Qprev – Qdef)*k , 

onde k nada mais é do que um conversor de unidades, de m3/s para hm3 e obtido por: 

k = [nº de dias no mês] * 24 * 3600/1000000 . 

Volume médio (VOLmed) = precisamos agora de um volume que seja representativo para o período. Para isso podemos utilizar a média entre os volumes inicial e final: VOLmed = (VOLini + VOLfin)/2 . 

Nível montante (NM) = corresponde ao valor do nível da água a montante da barragem da UHE. Esse valor pode ser obtido através de uma curva cota x volume, ou seja, a partir do volume do reservatório podemos determinar sua respectiva cota. Os coeficientes desse polinômio são dados pelo arquivo CadUsH.csv e nós já os organizamos na nossa tabela de dados da UHE. Quanto ao volume, acabamos de calcular um volume médio para o mês. Logo, basta aplicar a equação:  NM = A0 + (A1*VOLmed) + (A2*VOLmed^2) + (A3*VOLmed^3) + (A4*VOLmed^4) . 

Nível jusante (NJ) = corresponde ao valor do nível da água a jusante da barragem da UHE. Esse valor pode ser obtido pela curva cota x vazão, ou seja, a partir da vazão defluente podemos determinar sua respectiva cota. Os coeficientes desse polinômio são dados pelo arquivo CadUsH.csv e nós já os organizamos na nossa tabela de dados da UHE. Quanto  à vazão defluente, já a temos calculada. Logo basta aplicar a equação: NM = B0 + (B1*Qdef) + (B2*Qdef^2) + (B3*Qdef^3) + (B4*Qdef^4) . 

Altura bruta de queda (HB) = corresponde à queda d’água disponível para gerar energia e pode ser obtida pela diferença entre o nível de montante e o nível de jusante: HB = NM – NJ 

Altura líquida de queda (HL) = na altura líquida consideramos as perdas de energia do sistema hidráulico. Esse valor de perda pode ser disponibilizado em percentual ou em metros. No nosso caso, para a UHE Furnas, ele está disponibilizado em metros, logo a equação é bastante simples: HL = HB – perdas 

Produtibilidade (PRDT) = expressa a quantidade de MW gerados por m³/s de água turbinada, em função da queda líquida. Obtemos através da equação: PRDT = HL * produtibilidade específica 

Potência hidráulica (POT HIDRO) = corresponde a potência produzida pela UHE em função da vazão turbinada. Obtemos através da equação: POT HIDRO = PRDT * Qtur 

4. Inserindo uma UTE ao nosso modelo

Agora que a modelagem da nossa UHE está concluída, vamos incluir também uma UTE no modelo. Como a UHE de Furnas pertence ao subsistema SE, podemos escolher uma usina térmica do mesmo subsistema. Para este exemplo, utilizaremos a UTE Marlim Azul. Encontraremos os dados necessários dessa UTE na planilha Pilha_term_PMO e os copiaremos para a planilha do modelo, conforme mostrado na Imagem 5. 

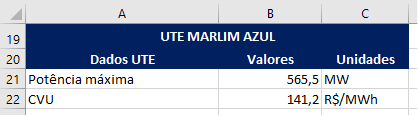
Dando continuidade, vamos agora estruturar os cálculos de operação da nossa UTE. Ao final desta etapa, devemos obter uma tabela semelhante à apresentada na Imagem 6, contendo as seguintes colunas: 

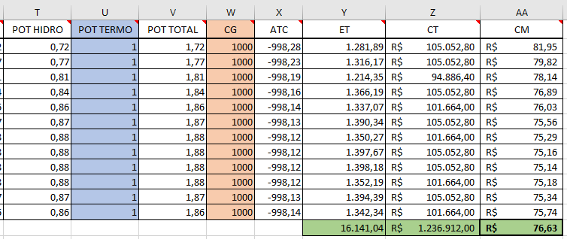
Potência térmica (POT TERMO) = corresponde a potência produzida pela UTE. Esse valor será definido posteriormente pelo algoritmo de otimização do Excel. Por ora, vamos preencher com um valor qualquer provisório, como o número 1, e deixar esse campo com outra cor para destacar. 

Potência total (POT TOTAL) = corresponde a soma da potência hidráulica e da potência térmica, dada por: POT TOTAL = POT HIDRO + POT TERMO 

Carga (CG) = representa a carga do sistema, isto é, o consumo energético que queremos atender com nossas usinas. Aqui encontramos outra dificuldade: prever o valor dessa carga futura. Novamente, discutir um modelo de previsão de carga não é nosso intuito, portanto vamos usar valores arbitrários para testar o modelo. Como nossa UHE pode gerar 912 MW e nossa UTE 565,5 MW, podemos testar algo como 1000 MW. No final poderemos variar esse valor à vontade para entender como o modelo muda a operação para anteder cargas maiores ou menores. 

Atendimento à carga (ATC) = este é um ponto fundamental no contexto da otimização: as restrições do modelo. No nosso caso, a potência total gerada precisa, obrigatoriamente, atender 100% da carga. Logo, a diferença entre potência total e carga deve ser igual a zero. Essa condição será imposta ao algoritmo como uma restrição, que veremos adiante como configurar. Por ora precisamos saber que a equação dessa coluna é: ATC = POT TOTAL – CG 

Energia Total (ET) = corresponde a quantidade de energia (em MWh) gerada ao longo do mês de referência. Para chegar a esse valor, multiplicamos a potência total instalada pelo número de dias do mês e, em seguida, por 24 horas, ou seja: ET = POT TOTAL * Dias no Mês * 24 

5. Otimização da operação

Agora chegamos ao passo final do nosso modelo. É aqui que tomaremos uma certa liberdade para definir como calcular os custos de operação, já que os modelos reais utilizados no SIN são muito mais sofisticados, incorporando custo marginal da operação, valor da água e várias outras complexidades. Para que possamos construir e executar tudo de forma tranquila no Excel, vamos simplificar esse aspecto e adotar uma representação mais direta do custo de geração no nosso modelo. 

Na prática, usinas hidrelétricas não possuem um custo explícito de combustível, pois sua energia provém da vazão natural do rio. Já as usinas térmicas têm um custo claro e mensurável, associado ao combustível utilizado, expresso pelo seu CVU. Assim, para manter o modelo simples e compreensível, vamos assumir que queremos calcular um custo médio da energia gerada ao longo do horizonte. Portanto vamos construir as seguintes colunas: 

Custo Total (CT) = como apenas as usinas térmicas possuem um custo explícito, utilizaremos esse valor para calcular o custo total de geração em cada mês:  CT = POT TERMO * Dias no Mês * 24 * CVU 

Custo Médio (CM) = por fim, o custo médio do modelo é dado pela relação entre o custo total e a energia total gerada: CM = CT/ET 

Agora que nossa tabela de cálculos está montada, precisamos apenas de mais um dado para finalizar a preparação do modelo: o volume inicial de armazenamento. O valor mais recente desse volume para cada UHE pode ser encontrado na planilha RDH. Entretanto, é importante lembrar que esse dado corresponde ao último dia observado — no nosso exemplo, 21/11/2025 — e não ao início de dezembro. Temos aqui, portanto mais uma dificuldade da modelagem, mas, novamente, para viabilizar o modelo, simplificaremos e adotaremos esse valor mais recente como sendo o volume inicial do mês, inserindo ele na planilha conforme a Imagem 7. 

Volume Inicial (%) = corresponde ou percentual de volume útil do reservatório e pode ser extraído da planilha RDH. 

Volume Inicial (hm3) = aqui precisamos converter o valor obtido do RDH de percentual para hm3, portanto aplicamos a seguinte equação: Volume Inicial = Vol. Mínimo + (Vol. Máximo – Vol. Mínimo) * Vol. Inicial % 

E, para finalizar iremos fazer o somatório das colunas de energia total e custo total, e fazer a relação entre elas para obter um custo médio de todo o horizonte de operação, que chamaremos de custo médio final e será dado por: CMF = ΣCT/ΣET 

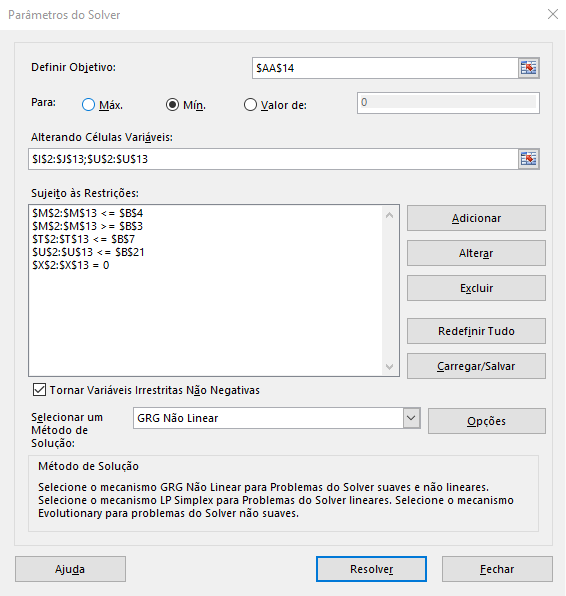
Com toda a tabela de cálculos preparada, podemos avançar para a etapa de otimização. Para isso, utilizaremos o Solver do Excel — uma ferramenta disponível na aba Dados e que, em alguns casos, precisa ser habilitada nas Opções do Excel antes de ser usada. 

Função Objetivo = o primeiro passo é indicar ao Solver qual é o objetivo da otimização. No nosso caso, queremos minimizar o custo médio final da operação. Esse será o valor que o Solver tentará reduzir ao máximo. 

Variáveis de Decisão = em seguida, informamos ao Solver quais células ele pode alterar durante o processo de busca pela solução ótima. Esses são justamente os campos que deixamos previamente destacados na tabela e são os campos de valores nos quais o modelo possui liberdade de ajuste. O Solver irá testar diferentes combinações desses valores até encontrar aquela que resulta no menor custo possível. 

Restrições = depois disso, precisamos estabelecer as restrições do modelo. As restrições garantem que as soluções encontradas pelo Solver respeitem as condições físicas e operacionais do sistema, como: 

• O volume final do reservatório deve ser inferior ao volume máximo e superior ao volume mínimo; 
• Tanto a potência hidráulica quanto a potência térmica têm de ser inferiores às potências máximas de suas respectivas usinas; 
• O atendimento a carga deve ser total, portanto seu valor deve ser igual a zero. 

Elas funcionam como “regras do jogo”, assegurando que o Solver não proponha soluções inviáveis ou fora da realidade operacional. 

Por fim, selecionamos o método GRG Não Linear, o mais adequado para lidar com equações contínuas e relações não lineares presentes no modelo hidrotérmico simplificado que construímos.  

Se você acompanhou tudo até aqui, a tela do seu Solver ficará semelhante a tela mostrada na Imagem 8. Com tudo configurado, basta executar a simulação e aguardar o Solver encontrar a combinação ótima de decisões para minimizar o custo total da operação.

Com o modelo concluído, podemos agora explorar diferentes cenários e análises. É possível simular variações de carga, testar novas séries de vazões previstas, alterar o conjunto de usinas em operação ou até mesmo inserir novas usinas no sistema. Esse ambiente flexível nos permite experimentar, comparar resultados e, sobretudo, compreender melhor os fundamentos de um modelo de despacho hidrotérmico.

Link para download da planilha do modelo: